The Herald has a story about hazards of coffee. The picture caption says
Men who drink more than four cups a day are 56 per cent more likely to die.
which is obviously not true: deaths, as we’ve observed before, are fixed at one per customer. The story says
It’s not that people are dying at a rapid rate. But men who drink more than four cups a day are 56 per cent more likely to die and women have double the chance compared with moderate drinkers, according to the The University of Queensland and the University of South Carolina study.
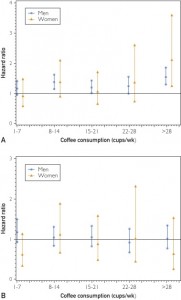
What the study actually reported was rates of death: over an average of 17 years, men who drink more than four cups a day died at about a 21% higher rate, with little evidence of any difference in men. After they considered only men and women under 55 (which they don’t say was something they had planned to do), and attempted to control for a whole bunch of other factors, the rate increase went to 56% for men, but with a huge amount of uncertainty. Here are their graphs showing the estimate and uncertainty for people under 55 (top panel) and over 55 (bottom panel)
There’s no suggestion of an increase in people over 55, and a lot of uncertainty in people under 55 about how death rates differed by coffee consumption. In this sort of situation you should ask what else is already known. This can’t have been the first study to look at death rates for different levels of coffee consumption. Looking at the PubMed research database, one of the first hits is a recent meta-analysis that puts together all the results they could find on this topic. They report
This meta-analysis provides quantitative evidence that coffee intake is inversely related to all cause and, probably, CVD mortality.
That is, averaging across all 23 studies, death rates were lower in people who drank more coffee, both men and women. It’s just possible that there’s an adverse effect only at very high doses, but the new study isn’t very convincing, because even at lower doses it doesn’t show the decrease in risk that the accumulated data show. So. The new coffee study has lots of uncertainty. We don’t know how many other ways they tried to chop up the data before they split it at age 55 — because they don’t say. Neither their article nor the press release gave any real information about past research, which turns out to disagree fairly strongly.
I agree. Beyond all this is the ubiquitous “Type M error” problem, also known as the statistical significance filter: By choosing to look at statistically significant results (i.e., those that are at least 2 standard errors from zero) we’re automatically biasing upward the estimated magnitudes of any comparisons. So, yeah, I don’t believe that number. I’d also like to pick on this quote from the linked news article:
“It could be the coffee, but it could just as easily be things that heavy coffee drinkers do,” says The University of Queensland’s Dr Carl Lavie. “We have no way of knowing the cause and effect.”
But it’s not just that. In addition, we have no good reason to believe this correlation exists in the general population. Also this:
Senior investigator Steven Blair of the University of South Carolina says it is significant the results do not show an association between coffee consumption and people older than 55. It is also important that death from cardiovascular disease is not a factor, he says.
Drawing such conclusions based on a comparison not being statistically significant, that’s a no-no too. On the plus side, it says “the statistics have been adjusted to remove the impact of smoking.” I hope they did a good job with that adjustment. Smoking is the elephant in the room. If you don’t adjust carefully for smoking and its interactions, you can pollute all the other estimates in your study. Let me conclude by saying that I’m not trying to pick on this particular study. These are general problems. It’s just helpful to consider them in the context of specific examples. There are really two things going on here. First, due to issues of selection, confounding, etc., the observed pattern might not be real. Second, even if it is real, the two-step process of first checking for statistical significance, then taking the unadjusted point estimate at face value, has big problems because it leads to consistent overestimation of effect sizes.
I’m posting this here (as well as on our statistics blog) because I think these points are relevant for political science research as well.